本文深入探讨了训练大规模语言模型所需的时间、资源及计算能力,尤其集中在Qwen2-72B模型的预训练过程。更新信息显示,Qwen2的技术报告已经发布,训练数据集已增加至7T,虽然训练语料的长度在最后阶段才从4096扩展至32768,但早期的预估算力需求可能会有一定程度的高估,但不会超过1.6倍。
背景
设想一下,如果某个高层管理人员把你叫到会议上,询问你是否能够在一个千卡集群上训练出一个Qwen、百灵、凤凰、ChatGLM或ChatGPT模型,你会如何回答?必然会首先给出一个肯定的答复:可以训练!然而,接下来的问题将涉及到数据需求、所需人力以及是否需要一个专门的工程团队来解决千卡架构的问题。
那么,最关心的第三个问题便是:训练一个大模型需要多久?在日常的算法训练中,我们通常会直接启动训练,观察tqdm进度条和loss曲线进行估算。但在会议上,显然不可能仅仅说“让我准备好数据和工程组,我先试试看跑几步。”
本文旨在解答这个关键问题:预训练一个模型到底需要多长时间。
结论
-
预训练Qwen2-72B模型,使用7T tokens数据集和6000张A100显卡,完整的epoch训练时间最多需要30天。训练语料长度的扩展是在预训练最后阶段进行的,虽然时间点并未明确,但因此形成的算力需求预估可能会有高估,但不会超过1.6倍。
-
计算量需求公式为3T(2.6e6s + 2P),其中T代表数据集的token数量,P为模型参数量,s表示序列长度。在较短序列长度下,公式简化为6TP。若使用全部重计算技术,则系数从3变为4。
-
大模型的计算量基本上只与“矩阵乘法”相关,并且反向传播过程的计算量是正向过程的两倍。不同的优化器对算力需求的影响微乎其微。
-
注意力机制对序列长度的平方复杂度影响,提升到32768的长度对于总算力需求的增加约为0.6倍。
-
batch size对计算量没有显著影响,当超过某一阈值后,对训练时间的影响亦不明显。
正文
基础概念科普:
FLOPS
定义:浮点运算次数每秒(Floating Point Operations Per Second),通常理解为硬件的计算性能。
注1:GPU的算力通常无法完全利用,涉及各种框架、并行、通信、调度和内存等概念。常见的结论是:
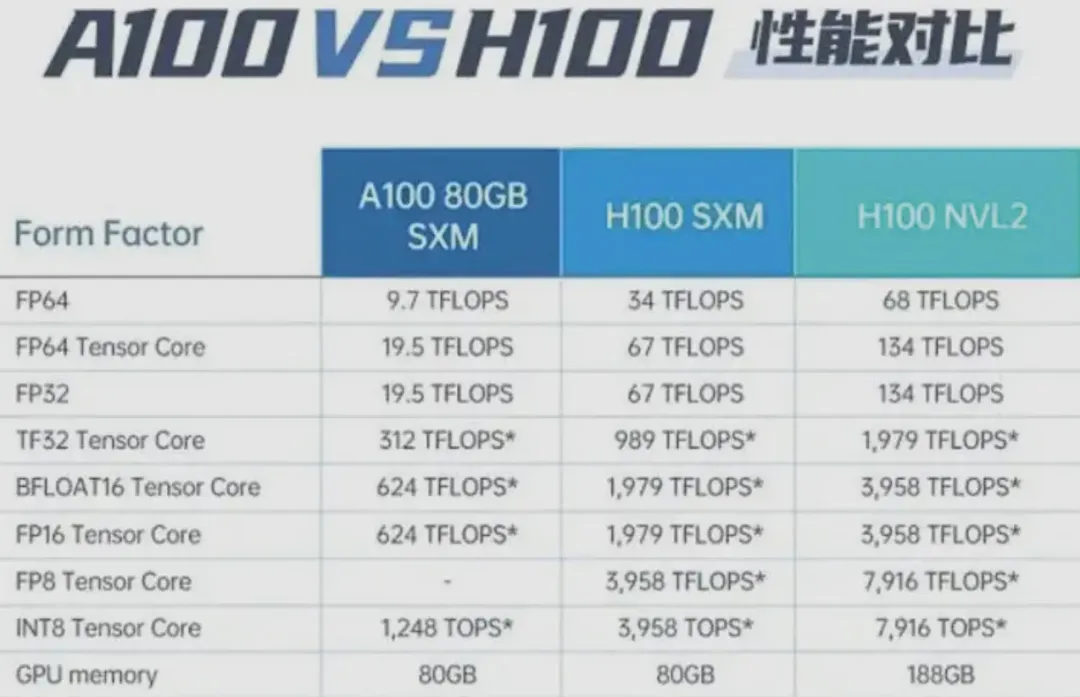
- A100显卡的单卡单精度利用率通常在25%到75%之间,取中间值约为300 TFLOPS。
- H100显卡的算力是A100的三倍以上,利用率需用最新的FlashAttention3来达到上限,一般可取1000 TFLOPS。
注2:同一GPU在不同精度运算时,其性能表现也是不一样的,这与硬件架构设计以及不同精度运算的实现有关。
详细原因可参考:
不同产品的计算能力:NVIDIA CUDA GPUs
计算能力解释:NVIDIA CUDA C Programming Guide

英伟达A100与H100及利用NVLink技术连接的两块H100显卡在不同精度下的FLOPS对比。
FLOPs
定义:浮点运算数量(Floating Point Operations),通常理解为训练大模型所需的算力,能够衡量算法及模型的复杂度。乘法与加法可视为相同。
1 MFLOPS(百万FLOPS)表示每秒一百万次浮点运算。
1 GFLOPS = 10^3 MFLOPS(十亿FLOPS),即每秒十亿次浮点运算。
1 TFLOPS = 10^3 GFLOPS(万亿FLOPS),即每秒一万亿次浮点运算。
1 PFLOPS = 10^3 TFLOPS(千万亿FLOPS),即每秒一千万亿次浮点运算。
1 EFLOPS = 10^3 PFLOPS(百京FLOPS),即每秒一百亿亿次浮点运算。
1 ZFLOPS = 10^3 EFLOPS(兆京FLOPS),即每秒十万京亿次浮点运算。
也是本文的主要内容。
MACs
定义:乘法加法累积操作次数(Multiply-Accumulate Operations),是深度学习领域的常见计算抽象,表示将两个数相乘并将乘积累加到一个累加器上。
也是描述大模型算力的单位。
根据定义,1 MACs ≈ 2 FLOPs。
MACs使用得不多的原因在于,正常大模型计算中,乘法与加法的运算量基本相同,因此不需单独计算。
硬件上矩阵乘法的算力需求
假设我们有矩阵A(a1 * a2)与矩阵B(b1 * b2)。我们需要计算C = A * B。
根据定义,a2 = b1,设为h。最终输出矩阵C的尺寸为a1 * b2。
如需回顾矩阵乘法的定义,可参考以下图示:
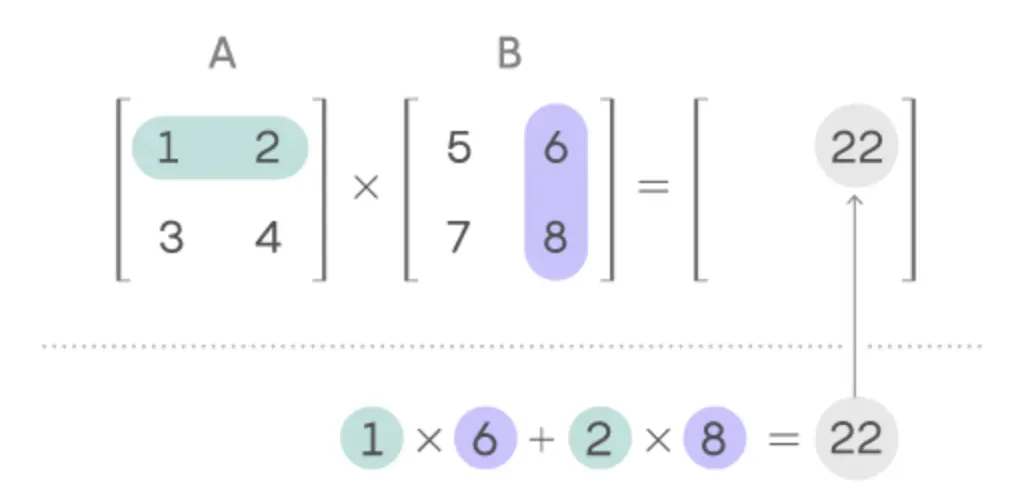
从C矩阵反推,每个元素都需要经历h次乘法和h次加法。即,2h FLOPs = 1h MACs。
注:这里之所以是h次加法,而不是h-1次,是因为硬件计算加法的本质是需放入累加器。因此即使是第一次乘法的结果也需要进行加法。
即,A * B的矩阵计算所需的算力为2 * h * a1 * b2 FLOPs,即2 * h * 输出矩阵的参数量 FLOPs。
大模型FLOPs计算
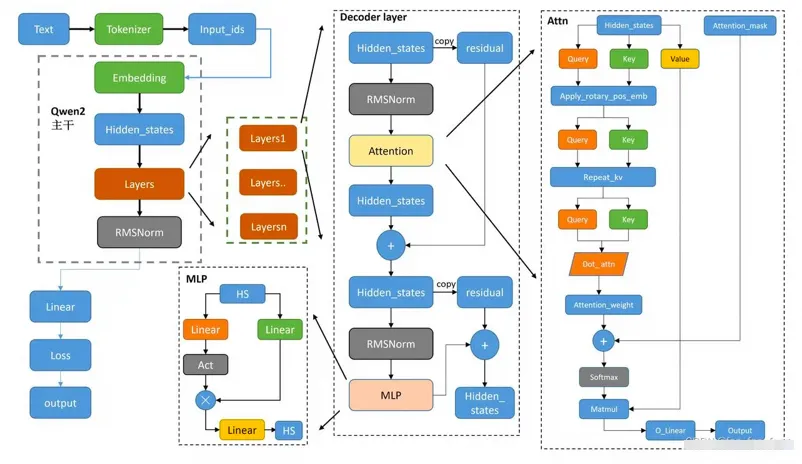
下面展示Qwen2-72B模型的架构图:
以下是一些模型参数:
{
"architectures": [
"Qwen2ForCausalLM"
],
"attention_dropout": 0.0,
"bos_token_id": 151643,
"eos_token_id": 151645,
"hidden_act": "silu",
"hidden_size": 8192,
"initializer_range": 0.02,
"intermediate_size": 29568,
"max_position_embeddings": 32768,
"max_window_layers": 80,
"model_type": "qwen2",
"num_attention_heads": 64,
"num_hidden_layers": 80,
"num_key_value_heads": 8,
"rms_norm_eps": 1e-06,
"rope_theta": 1000000.0,
"sliding_window": 131072,
"tie_word_embeddings": false,
"torch_dtype": "bfloat16",
"transformers_version": "4.40.1",
"use_cache": true,
"use_sliding_window": false,
"vocab_size": 152064
}
可以查看模型运算的Python文件:
前向计算过程
结论
大模型的算力需求基本上只与矩阵乘法相关。
提取出必要参数:
- batch size:用户自定义,假设为4
- seq length:取较大的长度32768
- hidden_size:隐藏层大小:8192
- num_hidden_layers:80
- vocab_size:词表大小:152064
Embedding层(参数量占比1.7%,算力需求占比0%)
输入:[batch size, seq length] 输出:[batch size, seq length, hidden size]
该层将输入的token序列映射为对应的embedding序列。
即需要查找每个输入token在词表中的embedding。涉及到一些position embedding的计算,例如输入序列长度超过max_position_embeddings时会临时计算新的position embedding,未超出则直接使用计算过的缓存等。但由于计算量极小,因此可忽略不计。
Transformer层(参数量占比96.6%,计算量占99%)
单个Transformer主要包括一个Attention块和一个FFN块,以及一些其他的杂项。
单个Attention块(参数量占比16%,计算量占48%)
class Qwen2Attention(nn.Module):
"""Multi-headed attention from 'Attention Is All You Need' paper.
Modified to use sliding window attention: Longformer and "Generating Long Sequences with Sparse Transformers".
"""
def __init__(self, config: Qwen2Config, layer_idx: Optional[int] = None):
super().__init__()
self.config = config
self.layer_idx = layer_idx
if layer_idx is None:
logger.warning_once(
f"Instantiating {self.__class__.__name__} without passing `layer_idx` is not recommended and will "
"to errors during the forward call, if caching is used. Please make sure to provide a `layer_idx` "
"when creating this class."
)
self.hidden_size = config.hidden_size
self.num_heads = config.num_attention_heads
self.head_dim = self.hidden_size // self.num_heads
self.num_key_value_heads = config.num_key_value_heads
self.num_key_value_groups = self.num_heads // self.num_key_value_heads
self.max_position_embeddings = config.max_position_embeddings
self.rope_theta = config.rope_theta
self.is_causal = True
self.attention_dropout = config.attention_dropout
if (self.head_dim * self.num_heads) != self.hidden_size:
raise ValueError(
f"hidden_size must be divisible by num_heads (got `hidden_size`: {self.hidden_size}"
f" and `num_heads`: {self.num_heads})."
)
self.q_proj = nn.Linear(self.hidden_size, self.num_heads * self.head_dim, bias=True)
self.k_proj = nn.Linear(self.hidden_size, self.num_key_value_heads * self.head_dim, bias=True)
self.v_proj = nn.Linear(self.hidden_size, self.num_key_value_heads * self.head_dim, bias=True)
self.o_proj = nn.Linear(self.num_heads * self.head_dim, self.hidden_size, bias=False)
self.rotary_emb = Qwen2RotaryEmbedding(
self.head_dim,
max_position_embeddings=self.max_position_embeddings,
base=self.rope_theta,
)
def forward(
self,
hidden_states: torch.Tensor,
attention_mask: Optional[torch.Tensor] = None,
position_ids: Optional[torch.LongTensor] = None,
past_key_value: Optional[Cache] = None,
output_attentions: bool = False,
use_cache: bool = False,
cache_position: Optional[torch.LongTensor] = None,
) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]:
bsz, q_len, _ = hidden_states.size()
query_states = self.q_proj(hidden_states)
key_states = self.k_proj(hidden_states)
value_states = self.v_proj(hidden_states)
query_states = query_states.view(bsz, q_len, self.num_heads, self.head_dim).transpose(1, 2)
key_states = key_states.view(bsz, q_len, self.num_key_value_heads, self.head_dim).transpose(1, 2)
value_states = value_states.view(bsz, q_len, self.num_key_value_heads, self.head_dim).transpose(1, 2)
kv_seq_len = key_states.shape[-2]
if past_key_value is not None:
if self.layer_idx is None:
raise ValueError(
f"The cache structure has changed since version v4.36. If you are using {self.__class__.__name__} "
"for auto-regressive decoding with k/v caching, please make sure to initialize the attention class "
"with a layer index."
)
kv_seq_len += past_key_value.get_usable_length(kv_seq_len, self.layer_idx)
cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)
query_states, key_states = apply_rotary_pos_emb(query_states, key_states, cos, sin, position_ids)
if past_key_value is not None:
cache_kwargs = {"sin": sin, "cos": cos, "cache_position": cache_position} # Specific to RoPE models
key_states, value_states = past_key_value.update(key_states, value_states, self.layer_idx, cache_kwargs)
# repeat k/v heads if n_kv_heads < n_heads
key_states = repeat_kv(key_states, self.num_key_value_groups)
value_states = repeat_kv(value_states, self.num_key_value_groups)
attn_weights = torch.matmul(query_states, key_states.transpose(2, 3)) / math.sqrt(self.head_dim)
if attn_weights.size() != (bsz, self.num_heads, q_len, kv_seq_len):
raise ValueError(
f"Attention weights should be of size {(bsz, self.num_heads, q_len, kv_seq_len)}, but is"
f" {attn_weights.size()}"
)
if attention_mask is not None: # no matter the length, we just slice it
causal_mask = attention_mask[:, :, :, : key_states.shape[-2]]
attn_weights = attn_weights + causal_mask
# upcast attention to fp32
attn_weights = nn.functional.softmax(attn_weights, dim=-1, dtype=torch.float32).to(query_states.dtype)
attn_weights = nn.functional.dropout(attn_weights, p=self.attention_dropout, training=self.training)
attn_output = torch.matmul(attn_weights, value_states)
if attn_output.size() != (bsz, self.num_heads, q_len, self.head_dim):
raise ValueError(
f"`attn_output` should be of size {(bsz, self.num_heads, q_len, self.head_dim)}, but is"
f" {attn_output.size()}"
)
attn_output = attn_output.transpose(1, 2).contiguous()
attn_output = attn_output.reshape(bsz, q_len, self.hidden_size)
attn_output = self.o_proj(attn_output)
if not output_attentions:
attn_weights = None
return attn_output, attn_weights, past_key_value
输入:[batch size, seq length, hidden size] 输出:[batch size, seq length, hidden size]
逐步解构:
- 将输入映射至三个矩阵Q、K、V(注意由于GQA,K、V矩阵较小的情况)。计算量为:2 * hidden_size * num_heads * head_dim * batch size * seq length ≈ 17.6 TFLOPs;
- K计算量减少num_attention_heads / num_key_value_heads倍,即2.2 TFLOPs;
- V同K,2.2 TFLOPs;
- 此外,应用旋转向量的计算量非常小;
- K、V矩阵扩展至num_attention_heads个头,计算量也很小;
- Q * K的计算量:batch size * num_heads * seq length * seq length ≈ 70 TFLOPs;
- 经过softmax的计算量:粗略估计为3 * 0.25 TFLOPs;
- 注意力矩阵 * V矩阵计算量:2 * seq length * batch size * num_heads * seq length * head_dim ≈ 70 TFLOPs;
- 线性层的计算量:2 * hidden_size * batch size * seq length * hidden_size ≈ 17.6 TFLOPs。
综上,Attention块的算力需求约为80层 * (17.6 TFLOPs + 2 * 2.2 TFLOPs + 70 TFLOPs + 0.25 TFLOPs + 3 * 0.25 TFLOPs + 70 TFLOPs + 17.6 TFLOPs) ≈ 14 PFLOPs。
计算公式可以简化为:num_hidden_layers * batch size * seq length * hidden size * (4.5 * hidden size + 4 * seq length)。
单个FFN块(参数量占比80%,计算量占51%)
# Copied from transformers.models.mistral.modeling_mistral.MistralMLP with Mistral->Qwen2
class Qwen2MLP(nn.Module):
def __init__(self, config):
super().__init__()
self.hidden_size = config.hidden_size
self.intermediate_size = config.intermediate_size
self.gate_proj = nn.Linear(self.hidden_size, self.intermediate_size, bias=False)
self.up_proj = nn.Linear(self.hidden_size, self.intermediate_size, bias=False)
self.down_proj = nn.Linear(self.intermediate_size, self.hidden_size, bias=False)
self.act_fn = ACT2FN[config.hidden_act]
def forward(self, hidden_state):
return self.down_proj(self.act_fn(self.gate_proj(hidden_state)) * self.up_proj(hidden_state))
输入:[batch size, seq length, hidden size] 输出:[batch size, seq length, hidden size]
实际上涉及的计算量只有一行代码,包含三次矩阵乘法、一次激活函数处理和一次矩阵点乘。
分析如下:
- 输入矩阵 * up_proj矩阵的计算量为:2 * batch size * seq length * hidden size * intermediate_size ≈ 63 TFLOPs;
- 输入矩阵 * gate_proj矩阵的计算量同第一步,约为63 TFLOPs;
- 经过激活函数的计算量几乎可以忽略;
- 矩阵点乘的计算量约为7 * c GLOPs(c为矩阵点乘的底层实现,预估在10以内);
- 上一步结果矩阵 * down_proj矩阵的计算量同第一步,约为63 TFLOPs。
综上,FFN层的算力需求约为80层 * (3 * 63 TFLOPs + 7 * c GLOPs) ≈ 15 PFLOPs。
计算公式可简化为:6 * batch size * seq length * hidden size * intermediate_size * num_hidden_layers。
其他杂项(参数量占比0%,计算量占0%)
# Copied from transformers.models.llama.modeling_llama.LlamaRMSNorm with Llama->Qwen2
class Qwen2RMSNorm(nn.Module):
def __init__(self, hidden_size, eps=1e-6):
"""Qwen2RMSNorm is equivalent to T5LayerNorm"""
super().__init__()
self.weight = nn.Parameter(torch.ones(hidden_size))
self.variance_epsilon = eps
def forward(self, hidden_states):
input_dtype = hidden_states.dtype
hidden_states = hidden_states.to(torch.float32)
variance = hidden_states.pow(2).mean(-1, keepdim=True)
hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon)
return self.weight * hidden_states.to(input_dtype
输入:[batch size, seq length, hidden size] 输出:[batch size, seq length, hidden size]
Qwen2的RMSNorm计算过程包括:
- 将数据转为双精度;
- 计算整个层输出向量的平方平均值向量variance,计算量大约为k * batch size * seq length * hidden size ≈ k * 10^9 FLOPs(k约为10);
- 对所有向量乘以向量variance的平方根倒数再加上eps,计算量约为2 * batch size * seq length * hidden size ≈ 2 * 10^9 FLOPs;
- 将数据转回原始精度,计算量大约为80 * 2 * (k + 2) GFLOPs。
输出层/分类头/Embedding逆映射(参数量占比1.7%,计算量占1%)
这里对输出Norm一下,(k + 2) GFLOPs。
再进行输出解码。
隐藏层状态 * [hidden size * vocab_size]的计算量为:2 * hidden_size * batch_size * seq_length * vocab_size ≈ 0.3 PFLOPs。
公式推导
算力主要来自于attention、FFN和解码过程。
算力合计汇总为:
batch size * seq length * hidden size * (2 * vocab_size + num_hidden_layers * (4.5 * hidden_size + 4 * seq_length + 6 * intermediate_size))
代入本文的例子Qwen2-72B。4 * 32768 * 8192 * (2 * 152064 + 80 * (4.5 * 8192 + 4 * 32768 + 6 * 29568)) = 29,991,378,670,845,952 ≈ 30 PFLOPs。
注:启用GQA后kv cache技术在继续生成阶段约能节约0.3 PFLOPs的计算量,影响不大。
为便于理解,公式可转变为:
bs * s * h(2V + L(4.5h + 4s + 6is))
其中,简写含义如下表所示。对已训练好的模型,用户能干预的只有batch size和seq length,而经验表明,intermediate_size通常与hidden size存在一定倍数关系。

进一步化简为:bs * s,假设只经过一轮epoch,即为全部数据的token数量。
由之前的分析可知,大模型绝大部分参数集中在输入输出两个embedding层和transformer层。具体来说,包括attention块和FFN块,以及两个词汇映射矩阵。以Qwen2为例,总体计算量为2 * h * V + h * L * (3 is + 2.25h)。
代入公式,得正向传播过程的总计算量为2T(2hLs + P),其中T为数据集的token数量,P为模型的参数量。M表示1e6,B表示1e9。
注1:这里公式中的s,即为注意力机制的平方复杂度影响。可以看出,仅当s长度超过三位数时,才会对大模型的执行时间产生明显影响。
注2:seq长度对大模型的影响并没有那么显著。以Qwen2为例,将seq提升到32768与seq长度为1的情况下,总算力需求仅扩大1.6倍,并不夸张。
数据验证
官方提供的部署效率信息如下图所示:

使用两张A100显卡,BF16精度下理论算力为1248 TFLOPS。通过公式计算大模型正向传播所需的算力:bs * s * (2.6M * s + 144B),设bs为1,s为1000 tokens。则一次正向输出的GPU时长计算为0.115秒,输出速度为8.67 qps,基本与图片中的8.48 qps一致。
拓展讨论:为何扩大batch size后,大模型输出速度先提高后保持不变
-
当batch size较小时,GPU能发挥的算力通常与batch size成正比。
- 这是因为在内存带宽上可能受到限制。
- GPU处理数据时,一个完整batch分为数据转移和数据计算两部分。数据转移部分需要占用内存带宽,转移完整的模型参数和一个batch的数据参数;而计算部分则与待计算数据量呈正相关。
- 在小batch情况下,转移完整模型参数的处理时间是固定的,因此随着batch size的增加,转移模型参数的时间占总处理时间的比例逐渐减少,导致效率逐渐提高。
- 理论上会出现一个batch size的切换点,超过该点后,显存占用增加,运算效率保持不变。但具体计算这个点的方式尚未明确。
-
当batch size达到一定大小,GPU的算力基本完全发挥时,调用大模型的训练时间已经与batch size无关。公式中并未涉及bs。
反向传播过程
结论:反向传播所需的算力通常是前向传播的2倍。
实验证据:
图片来源于笔者之前几篇文章的实验部分。
理论计算:
注:这里可以得到一个结论。为什么反向传播时,正向的矩阵乘法需要进行2次反向过程的矩阵乘法。
由于大模型的算力需求主要依赖于矩阵乘法,因此仅考虑涉及到矩阵乘法的反向传播梯度计算。
假设有简化模型流程,进行一次反向传播:
Y1 = W1 * X
Yo = W2 * Y1
L = loss(Yo,y)
我们通过模型输出Yo计算出的loss L,使用梯度下降法进行优化。首先计算Yo输出层对loss的梯度,即当前节点/层对最终输出的贡献。
这需要计算 △ Yo = d L / d Yo。这一步的计算量不大。接下来,需要计算出W2权重矩阵的责任,即计算d L / d W2 = △ Yo * Y1。这是第一次矩阵计算,每层都需要计算一次。
但尚未结束,因为模型是多层的,需往前推导,判定W1的责任。这需要计算 △ Y1 = d L / d Y1 = W2 * △ Yo。这是第二次矩阵计算,且每一层均需计算一次。
这两次矩阵计算的运算量与原先矩阵计算量一致。因大模型层数较多,虽然第一层不需要这一步,但影响很小。
实际上,一次矩阵计算(Yo = W2 * Y1)对应两次反向的矩阵计算(d L / d W2 = △ Yo * Y1)和(△ Y1 = d L / d Y1 = W2 * △ Yo),形成两倍关系。
梯度更新过程
梯度更新所需的计算量会依据优化器的不同而有所差异。例如,随机梯度下降法会对所有参数计算一次梯度乘以学习率,再计算一次结果加到参数权重。这意味着每个参数更新一次需要2 FLOPs。整个大模型一次更新需要2 * 72B FLOPs。虽然这个数字看似庞大,但与前向传播的计算量相比,可以忽略不计。
而对于Adam等带有二阶动量的优化器,计算公式较为复杂,计算量需求也会有所不同。

如上图所示,经过了5次公式计算,每个公式又需进行多次计算。但总体上,单个参数每次更新的计算量需求也是常数级别,针对前向传播的计算量可忽略。
数据验证
根据官方提供的数据集大小为7T tokens,序列长度最长为32768。假设大集群的算力利用率MFU为50%。代入公式,得出:
总计算量需求:3 * 7e12 * (2.6e6 * 32,768 + 144e9) FLOPs
单卡算力:300e12 FLOPS
需要的卡时为:15.93e9卡秒 ≈ 4,426,000卡小时 ≈ 180000卡天,即6,000张卡,30天能够完成一轮完整训练。
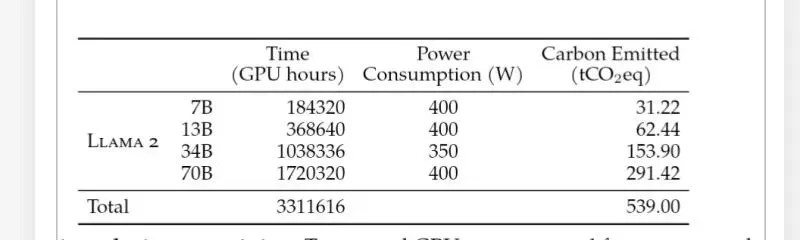
注:训练语料的长度在最终阶段才扩展至32768,因此本文的算力需求预估可能略高,最多不超过1.6倍。而与llama2训练过程的比较(Qwen2的模型架构与llama2相似),meta公司使用了1720320卡小时,context length为4096,2T数据集(Llama2)训练一个70B模型。与上述结论基本一致。
参考链接:
